bac + mention mécanique terminale
exercice 1	champ et force électrique - condensateur plan
Une charge q = 10 nC subit une force F d'intensité égale à 5µN. Quelle est l'intensité du champ électrique au point où est placée la charge ? Champ crée par une charge q ponctuelle. Quelle est l'intensité du champ électrique crée par une charge q=+2nC à 20 cm d'elle ? Un condensateur plan est constitué de deux armatures métalliques A et B, séparées par une lame d'air sec ; l'ensemble est chargé sous une tension U=5000V. Les armatures sont identiques et ont la forme d'un disque de faible épaisseur et de rayon R= 5 cm. A quelle distance minimale peut on rapprocher les armatures avant que l'air ne devienne conducteur ? La distance entre les armatures est portée à d=15 mm. Quelle est l'intensité du champ électrique E ? Ce champ est-il uniforme. Si l'intensité du champ entre les armatures est donnée par : E = Q/(eo.S), quelle est la valeur de la charge Q portée par chaque armature ?  Champ de claquage dans l'air sec : Ec = 3KV/mm. eo = 1/(36p) * 10-9 F/m.
corrigé
champ électrique et force sont proportionnels : F=qE E=5 10-6 / 10 10-9= 500 Vm-1. E =9 109 Q/ distance ² E= 9 109 *2 10-9 /0,2² = 450 Vm-1. E (Vm-1) = U (V) / distance (m) 5000/ distance < 3000 ; distance >5/3 mmm E=5000/0,015 =3,33 105 V m-1. Ce champ est uniforme sauf au voisinage des bords des plaques Q(coulomb)= Ee0S avec S=3,14 *25 10-4 =7,85 10-3 m² Q= 3,33 105 /(36*3,14)*10-9 *7,85 10-3 = 2,3 10-8 C
exercice2	plan incliné et frottements
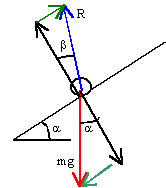
Un objet de masse m=20 kg, glisse le long d'une ligne de plus grande pente d'un plan incline d'un angle a=30° par rapport a l'horizontale. La somme du vecteur R, supposée constante, des forces de contact réparties en surface et exercées par le plan sur l'objet, fait un angle b avec la normale au plan. Exprimer le vecteur accélération du mobile en fonction de a, b, m, R, et g. Laché sans vitesse initiale, ce mobile parcourt une distance d=5 m en une durée t=1,7 s. Calculer l'accélération. Calculer l'angle b et la valeur du vecteur R.
..
corrigé
somme des forces sur un axe parallèle au plan dirigé vers le bas mg sin(a)-R sin(b) = ma a=g sin(a)-R/m sin(b) sur un axe perpendiculaire au plan mg cos(a)-R cos(b) =0 pas de décollage R sin(b) =m( g sin(a)-a) et R cos(b)=mg cos(a) tan(b)=(g sin(a)-a) / g cos(a). d=0,5 at² d'où a=10/1,7²= 3,46 ms-2. b = 9,63° ; R= 172 N
exercice 3	accélération : voiture sur un plan incliné
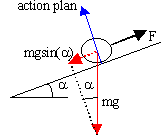
La masse d'une voiture est de 980 kg.Au démarrage, le moteur exerce un effort de traction de 450 Newtons. Quelle est l'accélération ? sur une route horizontale. sur une route qui s'élève de 2 mètres par 100 mètres. Pour estimer les forces de frottement sur une automobile (m=1450 kg) roulant à 60 kmh-1 sur une route horizontale, on accélère jusqu'à 65 kmh-1 puis on débraye. La voiture ralentit jusqu'à 55 kmh-1 en 7,2 s. Calculer la valeur de la sommes des forces de frottement en la supposant constante.
corrigé
somme vecteurs forces = masse * vecteur accélération route horizontale : a=450/980= 0,46 ms-2. montée du plan incliné sin(a)=0,02 450-980*9,8*0,02 = 980 a a = 0,26 ms-2. Exprimer les vitesses en ms-1. 65/3,6= 18,055 ms-1. 55/3,6= 15,277 ms-1. accélération ms-2=variation vitesse ms-1 / durée de la variation s a=(15,277-18,055)/7,2= - 0,386 ms-2. colinéaire à la vitesse mais de sens contraire projection de la somme des forces su un axe colinéaire à la vitesse norme des frottements=1450*0,386= 559 N
exercice 4	saut à l'élastique
Pour préparer un de ses futurs sauts à l'élastique, un sauteur veut tester la possibilité de sauter d'un pont au-dessus d'une rivière et d'effleurer, la surface de l'eau avec ses cheveux au cours de son saut. Il cherche à derterminer la longueur à vide l0 de l'élastique qu'il va utiliser pour atteindre son objectif. La masse m du sauteur =80 kg, la distance qui sépare le tablier du pont de la surface de l'eau est h= 22 m. L'élastique est caractérisé par une force de rappel T=µ[(l-l0)/l0], où µ désigne une constante positive égale à 5.103 N. l : longueur de l'élastique tendu. g=10 m/s² Une extrémité du fil est fixée au tablier du pont en un point fixe O origine d'un repère dont l'axe vertical Oz sera dirigé vers le haut.L'autre extrémité du fil, notée M est reliée à une masse m (égale à celle du sauteur équipé), que l'on supposera ponctuelle et libérée depuis le point O sans vitesse initiale. On posera OM = z Donner l'expression de ze, correspondant à la position d'équilibre de la masse m accrochée à l'élastique.On pourra poser A=mg/µ. Calculer le rapport ze/l0. Donner l'expression de l'énergie potentielle Ep d'intéraction du système {masse m, Terre, élastique} en fonction de la variable z et des données du problème, en prenant par convention Ep(z=0)=0. On sera amené à distinguer deux intervalles de variation de z et on tiendra compte de la continuité de la fonction Ep. En déduire, en fonction de la variable z l'expression de v² pendant les deux phases de la chute (v désignant la vitesse de la masse m). Exprimer la valeur de z1, point le plus bas en fonction de l0 et A. En déduire l'expression de l0, longueur à vide de l'élastique que devra utiliser le sauteur s'il veut atteindre son objectif, en focntion de h et A. Calculer numériquement l0 et l(e) longueur de l'élastique à l'équilibre.
corrigé
A l'équilibre le poids du sauteur est opposé à la tension de l'élastique. mg = m(ze-l0)/l0 . mg/m = ze /l0- 1 . A+1 = ze /l0 = 80*10/5000 + 1 = 1,16 énergie potentielle élastique non tendu : |z| < l0 : E potentielle de pesanteur mgz élastique tendu : |z|> l0 : E potentielle de pesanteur mgz + énergie potentielle élastique 0,5 m/l0( |z|-l0)²comme pour un ressort 0,5 kx² L'énergie potentielle de pesanteur est convertie en énergie cinétique et en énergie potentielle élastique stockée par le ressort . mg|z| = 0,5 mv²+ 0,5 m/l0( |z|-l0)² |z| < l0 : v²= 2g|z| |z|> l0 : v²= 2g|z| - m/(ml0) ( |z|-l0)² z1: point le plus bas la vitesse est nulle 2g|z1| = m/(ml0) ( |z1|-l0)² z1² -2l0(1+A)z1 + l0²=0 la résolution de cette équation donne z1 = 1,75 l0 . l'autre solution n'est pas à retenir car elle conduit à z1 inférieur à l0. l0=22/1,75 = 12,57 m ; ze= 1,16*12,57 =14,58 m
exercice 5	voyageur en retard
Un voyageur en retard court le long du quai à la vitesse constante V= 6 m.s-1. Quand il est à 20m du dernier wagon du train qui démarre avec une accélération constante a= +1 m.s-2 ( le train et le voyageur ont des trajectoires rectilignes parallèles.) Définir le repère dans lequel le mouvement est étudié. Préciser su le schéma les positions, les dates et les vitesses connues. Ecrire dans un même repère les équations horaires du voyageur et du dernier wagon considérés comme des points matériels. Montrer que le voyager ne peut pas rattraper le train . Quelle sera la distance minimale entre le voyageur et le dernier wagon?
corrigé
pour t=0 lorsque le train démarre.; X0=0 position du dernier wagon abscisse voyageur x1=6t-20 abscisse dernier wagon x2=0,5.a.t²=0,5 t² si le voyageur ratrappe le train x1=x2 ; 0,5 t²-6t+20=0 D=36-40, est négatif donc il n'y a pas de solution à notre équation ; le voyageur ne rattrapera jamais le train. Distance entre le dernier wagon et le voyageur : x2-x1 =0,5 t²-6t+20 Cette distance est minimale lorsque la dérivée par rapport au temps de cette fonction s'annule. t-6=0 ; t = 6 secondes x2-x1 = 0,5*6²-6*6+20 = 2 m
exercice 6	freinage d'un camion
Un camion de masse 3 tonnes roule sur une route à une vitesse de 72 km/h. On peut l'arrêter par freinage sur une distance de 50 mètres. Calculer: son énergie cinétique. l'intensité de la force constante qui produirait le même effet que les freins. la décélération, supposée constante, pendant le freinage.
corrigé
vitesse 75/3,6 = 20 ms-1. Energie cinétique = 0,5 m v² = 0,5 *3000*20²=6 105 Joules la variation d'énergie cinétique est égale au travail des forces de freinage 0- 0,5 m v²= -F* distance F=6 105 /50 = 12 000 N La somme vectorielle des forces et le vecteur accélération sont colinèaires et de sens contraire. valeur de la décélération : 12 000 /3000 = 4 ms-2. retour - menu