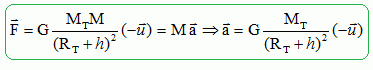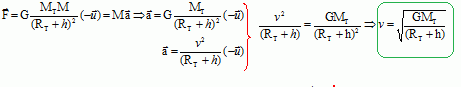I
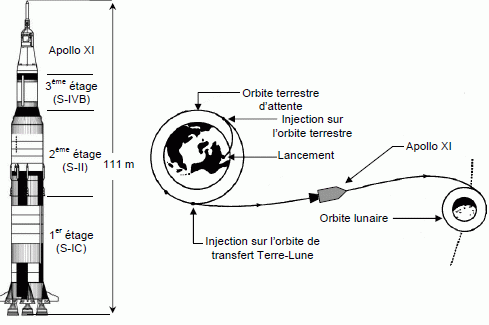
Le 16 juillet 1969 à
14 h 32 (heure française), la fusée géante américaine Saturn
V décolle de Cap Kennedy (Etats-Unis) avec à son sommet le
vaisseau
spatial "Apollo XI" et son équipage composé de Neil Armstrong, Edwin
Aldrin et Michael Collins. Le 21 juillet 1969 à 3 h 56, Armstrong est
le
premier homme à fouler le sol lunaire suivi quelques minutes plus tard
par
Aldrin. Les deux astronautes resteront en tout 22 heures sur la Lune, dont environ 2
heures à
l'extérieur du module d’exploration lunaire LEM.
Données :
Masse
de la Terre MT
= 5,98 x
10 24 kg
Rayon
de la Terre RT
= 6,37 x
10 3 km
Masse
de la Lune ML
= 7,35 x
10 22 kg
Constante de gravitation
universelle G
= 6,67 x10 – 11 m3.s
–
2.kg – 1 .
Champ de pesanteur
terrestre au niveau
du sol g = 9,8 m.s – 2
Masse totale de la fusée au
décollage : M = 2,9 x
10 3 tonnes
Tous les astres sont considérés comme
des corps à répartition de masse à symétrie sphérique.
On se propose
d’étudier d’une manière
simplifiée quelques unes des phases du voyage conduisant de la Terre à la Lune
ainsi que certaines
expériences scientifiques liées à la mission Apollo.
Ascension de la fusée Saturn
V
Le premier
étage (S-IC) fonctionne
pendant 180 secondes, il contient environ 2 tonnes de carburant et
d’oxygène
liquide permettant de propulser l’ensemble à une altitude de 68 km. L'intensité
de la
force de poussée F des réacteurs est de l’ordre de 3,3 x 10 7
N.
L’étude du
lancement de la fusée peut se
faire en appliquant la seconde loi de Newton dans certaines conditions
qu’on se
propose de préciser à partir de son énoncé ci-dessous :
« Dans
un référentiel galiléen, la
somme vectorielle des forces extérieures appliquées à un solide de
masse m
constante est égale au produit de la masse du solide par le vecteur
accélération de son centre d’inertie ».
Quel
référentiel supposé galiléen peut-on choisir pour étudier la phase du
début du
lancement ?
On peut utiliser un référentiel terrestre ou le référentiel
géocentrique au début du lancement.
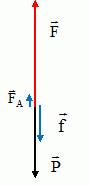
Faire
un inventaire des forces extérieures appliquées à la fusée en tenant
compte de
l’interaction de l’air avec la fusée. Les représenter au centre
d’inertie de la
fusée sur un schéma sans souci d’échelle (le décollage est supposé
vertical).
|
|
Le
poids P, la poussée des moteurs F, les forces de frottements f sur les
couches d'air, la poussée d'Archimède FA due à
l'air.
|
Pourquoi
ne peut-on pas appliquer la seconde loi de Newton, telle qu’elle est
énoncée, à
la fusée lors de son ascension ?
Les moteurs consomment du carburant et du comburant ( dioxygène liquide
) au décollage : la masse de la fusée n'est pas constante.
Quelle
hypothèse peut-on, cependant, poser pour appliquer cette loi au tout
début du
lancement ?
Sur une durée aussi petite que possible, la masse de la fusée est
à peu près constante.
En ne considérant
que le poids et la poussée, montrer que la valeur de
l’accélération de la fusée à l’instant initial du lancement vaut 1,6 m.s-2.
On écrit la seconde loi de Newton sur un axe orienté vers le
haut : F-P = M a.
F-Mg=Ma ; a = F / M -g
; M = 2,9
x
10 3 tonnes =2,9 106 kg.
a = 3,3 x 10 7
/ 2,9 106
-9,8 =1,579 ~1,6 m s-2.
Mise
en orbite autour de la
Terre du système {S-IVB +
Apollo XI}
A 68 km d’altitude,
les
réservoirs vides du premier étage sont largués et les cinq moteurs du
deuxième
étage sont allumés pendant 360 s. Après largage du deuxième étage,
l’unique
moteur du troisième étage est mis en fonction pendant 180 s permettant
la
satellisation sur une orbite circulaire d’attente à l’altitude h = 185 km.
Dans la
suite, on note {fusée} le système formé du troisième étage
et du vaisseau Apollo XI.
On étudie le
mouvement du système {fusée}, de centre
d’inertie G et de
masse m, dans le référentiel géocentrique supposé galiléen. On ne
tiendra
compte que de l’attraction gravitationnelle exercée par la Terre sur le
système
{fusée}.
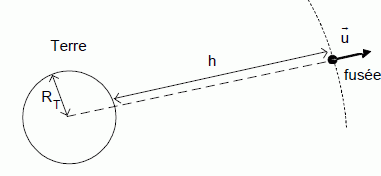
Donner
l’expression vectorielle de la force exercée par la Terre sur le système
{fusée}
en utilisant le vecteur unitaire défini sur la
figure. Reproduire la figure sur la copie et représenter cette force
(sans souci d'échelle).
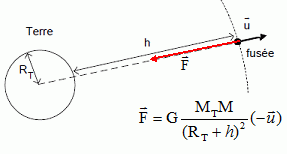
En appliquant la
deuxième
loi de Newton, établir l'expression vectorielle de l'accélération du
centre
d’inertie du système {fusée}. En supposant que le mouvement du système
{fusée}
est circulaire dans le référentiel géocentrique, montrer que le vecteur
accélération est centripète. En déduire que le mouvement est uniforme.
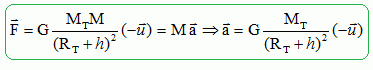
Le vecteur accélération est colinéaire au
vecteur unitaire et de sens contraire ; le vecteur accélération
étant dirigé vers le centre de la Terre est centripète.
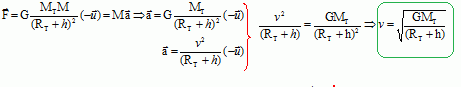
La valeur de la vitesse étant constante, le mouvement est
uniforme.
Calculer la
valeur de la vitesse du centre d’inertie G du système {fusée}.
RT+h =6,37 x
10 3 +185 km =6,555 106 m
v =[6,67 10-11
*5,98 x
10 24 / 6,555 106]½=7,80 103
m/s = 7,80 km/s ~
7,8 km/s.
Quelques expériences
associées à la mission Apollo
Lors de la mission Apollo
XI
et des suivantes, du matériel scientifique a été déployé à la surface
de la Lune
afin de l’étudier. Des
échantillons de roche lunaire ont également été ramenés sur Terre.
De
nombreuses méthodes de datation reposent sur la décroissance
radioactive de
certains radioéléments. Un radioélément est adapté à cette mesure si
son temps
de demi-vie est de l’ordre de grandeur de l’âge à déterminer.
Parmi les radioéléments ci-dessous, indiquer en justifiant celui
qui pourrait être utilisé pour mesurer l’âge de la Lune.
isotope radioactif
|
ordre de grandeur du temps de demi-vie
|
iode 131
|
une dizaine de jours
|
plutonium 238
|
une centaine d'années
|
potassium 40
|
un milliard d'années
|
La demi-vie de l'élément radioactif doit être du même ordre de grandeur que l'aêge de la Lune ( 4,5 109 ans). Parmi les trois isotpes cités, seul le potassium 40 convient.
Pour déterminer l'âge
des roches lunaires ramenées sur Terre par les astronautes, les physiciens ont mesuré
expérimentalement les quantités relatives d'argon 40 gazeux et de potassium 40
solide emprisonnés dans la roche lunaire.
Le potassium 4019K est un isotope
radioactif. Il se désintègre en produisant de l’argon 4018Ar.
Écrire l’équation de désintégration nucléaire d’un
noyau de potassium 40.
4019K ---> 4018Ar + 01e.
Donner
l’expression du nombre NK(t)
de noyaux radioactifs de potassium 40 présents dans l’échantillon de roche
lunaire à la date t en fonction du
nombre initial NK(0) de
ces noyaux.
La loi de décroissance radioactive s'écrit : NK(t) = NK(0) exp (-lt) ; l : constante radioactive du potassium 40.
|
|
Donner
la définition du temps de demi-vie d’un échantillon radioactif.
Durée au bout de laquelle l'activité initiale a diminué de moitié
; durée au bout de laquelle la moitié des noyaux initiaux se sont
désintégrés.
Établir la
relation liant la constante de désintégration
radioactive l et le temps de demi-vie. Montrer que l= 5,50 x 10 – 10 an – 1 pour le potassium 40 sachant que t1/2 = 1,26 x 10 9 ans.
NK(t) = NK(0) exp (-lt)
NK(t½) = 0,5 NK(0)
0,5 NK(0) = NK(0) exp (-lt½)
0,5 = exp (-lt½) ; ln 0,5 = -ln2 = -lt½ ; lt½ = ln 2.
l = ln2 / 1,26 109 = 5,50 10-10 an-1.
Un échantillon de 1,0 g de roche lunaire analysé
à la date t contient NAr(t) = 2,3 x10 17 noyaux d'argon 40 et NK(t) = 2,4 x10 16 noyaux
de potassium 40. En admettant que le potassium 40 ne subit que la
désintégration précédente et que la roche lunaire ne contenait pas
d’argon 40 au moment de sa formation, on montre que : NK(0) = NK(t) + NAr(t).
Évaluer
l’âge de cette roche lunaire.
NK(0) / NK(t) = exp(lt)
ln (NK(0) / NK(t) ) = lt
t = ln (NK(0) / NK(t) ) / l ;
NK(0) = NK(t) + NAr(t) = 2,4 x10 16 +2,3 x10 17=2,54 1017.
NK(0) / NK(t) =2,54 1017 / 2,4 x10 16= 10,58
ln (NK(0) / NK(t) ) = ln 10,58 =2,359
t = 2,359 / 5,50 10-10 =4,3 109 ans.
|