|
Un mobile M est animé
d'un mouvement rectiligne. On relève par intervalle
de temps régulier t
=1s, sa position L sur l'axe
x'x. On admet que la vitesse V à l'instant (t) est
:
V = [ X(t+1) - X(t-1) ] / (
2 t)
avec X(t) : abscisse du centre de
gravité du mobile.
|
date t(s)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
abscisse ( m)
|
1
|
2,2
|
3,8
|
5,8
|
8,2
|
10,2
|
12,6
|
14,6
|
|
vitesse (m/s)
|
xxxxxxxxxx
|
1,4
|
1,8
|
2,2
|
2,2
|
2,2
|
2,2
|
xxxxxx
|
Calcul de la vitesse à la
date :
|
|
- t= 1 s
:
(3,8-1) / 2 =
1,4 m/s.
- t= 2 s
:
(5,8-2,2) / 2 =
1,8 m/s.
- t= 3 s
:
(8,2-3,8) / 2 =
2,2 m/s.
- t= 4 s
:
(10,2-5,8) / 2
= 2,2 m/s.
- t= 5 s
:
(12,6-8,2) / 2
= 2,2 m/s.
- t= 6 s
:
(14,6-10,2) / 2
= 2,2 m/s.
|
|
|
Tracer la courbe
V(t) en fonction du temps et en déduire la
vitesse initiale V0.
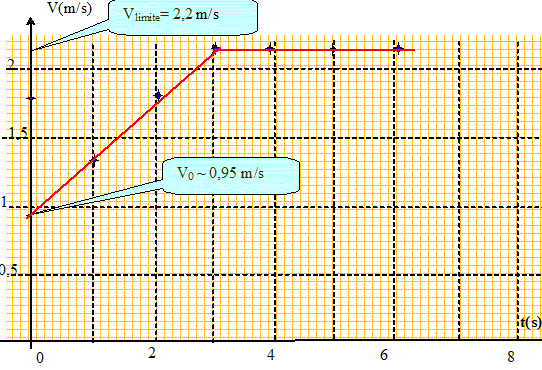
Identifier les
différentes phases du
mouvement.
- t < 3 s : phase transitoire,
mouvement rectiligne uniformément
accéléré,
- t > = 3 s : mouvement rectiligne
uniforme ( vitesse constante 2,2
m/s).
|
Calculer pour chaque phase du
mouvement l'accélération du
mobile.
L'accélération est une mesure de la
variation de vitesse du mobile.
a = DV/Dt.
Graphiquement on la détermine en calculant le
coefficient directeur de chaque droite
- Régime transitoire :
(2,2-0,95) / 3 ~ 0,42
m s-2.
- Mouvement rectiligne uniforme :
DV=0 donc
a
=0.
|
|
Etablir les
équations horaires du mouvement du mobile
M.
Régime
transitoire :
La vitesse est une primitive de
l'accélération : v(t) = a(t) +
Constante
On détermine la constante à partir
de la vitesse initiale V0=0,95 m/s
v(0) = constante = V0.
d'où v(t) = at + V0 =
0,42 t +
0,95.
.
|
La position est une primitive de la vitesse : x(t) =
½at2 + vt + constante.
On détermine la constante à partir de la
position initiale x0=1 m
1 = 0 + 0 + constante.
d'où : x(t)
= 0,21
t2 + 0,95 t+1.
Régime
permanent :
mouvement rectiligne uniforme : x(t) = 2,2 (t-3) +
constante.
On détermine la constante, par exemple à
t=3 s, x= 5,8 m.
5,8 = 2,2*0 + constante.
x(t) = 2,2(t-3) +
5,8.
Calculer la date
t1 à laquelle le mobile M passe par la
position L=4
m.
Le mouvement rectiligne uniforme
n'étant atteint qu'à partir d'une distance
L=5,8m, à la date t1 le mobile se trouve dans la
phase transitoire.
x(t) =
0,21 t2 + 0,95
t+1.
4 = 0,21 t12 + 0,95 t1
+1.
0,21 t12 + 0,95 t1 -3
=0
D= 0,952
-4*0,21*(-3) =3,42 ; D½=1,85.
t1 = (-0,95 + 1,85) / (2*0,21) = 2,14 s ~
2,1 s.
On ne retient pas la valeur négative pour une
durée.
|
