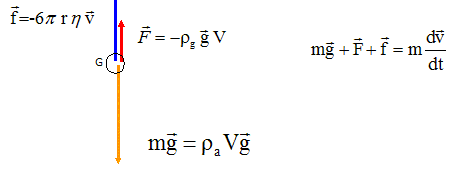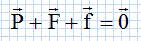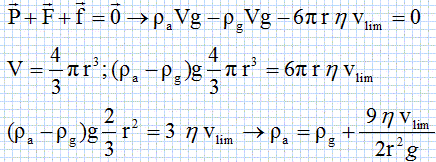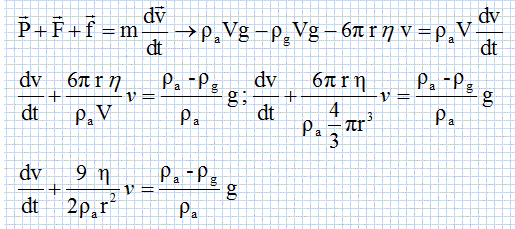La bille est utilisée dans un dispositif appelé viscosimètre
de Hoepler. Il se compose d'un long tube de verre vertical,
rempli d'un liquide visqueux ( glycérine ), dans lequel on laisse
tomber la bille. La viscosité renseigne sur la résistance d'un fluide
à s'écouler. La durée de chute Dt
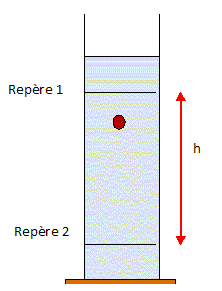
correspondant à une distance de chute h connue est mesurée à
l'aide de deux capteurs reliés à un chronomètre électronique. Les
deux capteurs sont repérés par les positions D et F comme le montre le schéma ci-dessous.
rayon de la bille r = 1,0 cm ; masse volumique de la bille ra (kg m-3) ; masse volumique de la glycérine rg = 1,26 103 kg m-3.
Viscosité de la glycérine h = 1,48 SI.
Etude des forces s'exerçant sur la bille :
On
étudie le mouvement de la bille dans le référentiel terrestre considéré
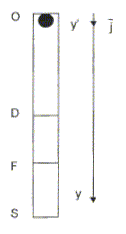
comme galiléen muni d'un repère (O, j ). O est l'origine du repère..
Son vecteur unitaire est orienté vers le bas. La bille totalement
immergée dans le liquide, est abandonnée du point O, sans vitesse
initiale. Son volume est noté V.
Représenter sur un
schéma les forces qui s'exercent sur la bille lors de
la chute.
Les grandeurs écrites
en gras et en bleu sont des
vecteurs.
Au cours de la chute la bille est
soumise aux forces suivantes :
- son poids
P,
la poussée d'Archimède
F
exercée par la glycérine, la force de
frottement fluide modélisée par
f
=
-kv
avec k = 6prh
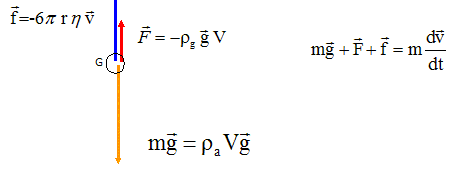
Exprimer littéralement la valeur P du poids de la bille.
P = m g avec m = raV ; P = m raV.
Exprimer littéralement la valeur F de la poussée d'Archimède.
F = g rgV.
La valeur de la force de frottement fluide est f = 6prhv.
Par une analyse dimentionnelle, donner l'unité de h.
|
h =f / (6prv)
6 p : sans dimension ; r : longueur : [r] =L ; v : vitesse= longueur / temps : [v] =L T-1.
f : force = masse x accélération = masse x longueur / temps2 : [ f ] = M L T-2.
[ h] = M L T-2 L-2 T soit M L-1 T-1 ou Pa s. |
Vitesse limite.
Lors de la chute, la bille atteint rapidement sa vitesse limite vlim avant son passage au niveau du repère R1.
Quel est le mouvement de la bille entre les deux repères. Justifier.
La
valeur de la vitesse est constante et le mouvement est rectiligne : le
mouvement de la bille est rectiligne uniforme entre les deux repères.
Quelle est la relation vectorielle liant les forces appliquées à la bille ? Justifier.
D"après
le principe d'inertie, la bille est pseudo-isolée : la somme
vectorielle des forces appliquées à la bille est nulle.
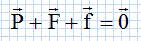
On mesure la durée de la chute de la bille entre les repères distants d'une hauteur h =40,0 cm. On obtient Dt = 0,41 s.
Calculer la vitesse limite vlim de la bille.
vlim = h / Dt =0,400 / 0,41 = 0,9756 ~0,98 m/s.
La courbe v = f(t) permet de mettre en évidence deux régimes distincts pour le mouvement de la bille.
Nommer ces deux régimes et déterminer graphiquement la vitesse limite de la bille. 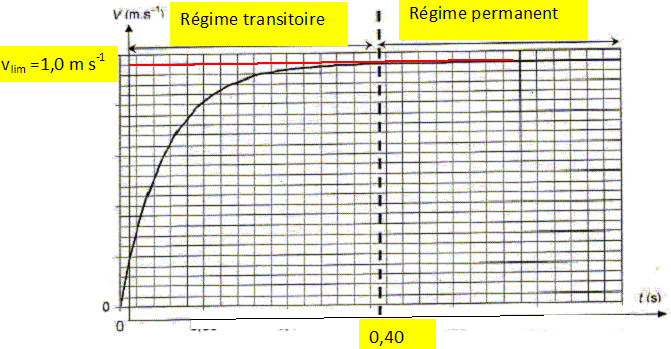
Proposer un protocol expérimental permettant d'obtenir la courne ci-dessus.
A l'instant du lacher de la bille, une acquisition vidéo assurée par une webcam
couplée à un ordinateur est déclenchée de manière à enregistrer 25 images par
seconde.
La vidéo est ensuite analysée à l'aide d'un logiciel approprié qui permet de
repérer aux dates t i les positions successives x i de G
lors de son mouvement descendant et de calculer approximativement la vitesse
moyenne v i entre les dates t i -1 et t i +
1.
En projetant la relation vectorielle établie dans le repère, exprimer puis calculer la masse volumique de la bille.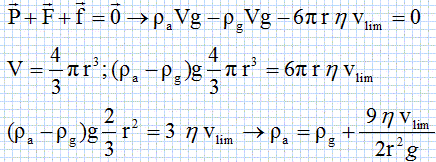
ra = 1,26 103 + 9*1,48 *0,98 / (2 10-4*9,8) = 7,85 103 kg m-3 ( acier ).
Etude théorique du mouvement de la bille.
A l'instant choisi comme origine des dates, la bille est abandonnée sans vitesse initiale au point O.
En utilisant la deuxième
loi de Newton montrer que l'équation
différentielle liant la vitesse de la bille et sa
dérivée par rapport au temps est de la forme
:
dv/dt + Av = B. 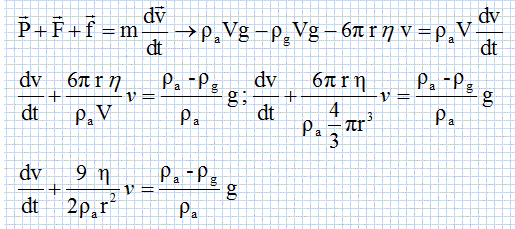
A = 9h / (2ra r2) = 9*1,48 / (2* 7,85 103 10-4) =8,48 s-1.
B =(1-rg/ra)g = (1-1,26 / 7,85) *9,8 = 8,23 m s-2.
Exprimer la vitesse limite en fonction de A et B. Calculer vlim.
dvlim /dt = 0 ; A vlim = B ; vlim = B/A =8,23 / 8,48 = 0,97 m s-1.
|
La courbe d'évolution de la vitesse au cours du temps peut être tracée par la méthode itérative d''Euler.
dv /dt +Av = B s'écrit : a +Av = B ( a ; accélération )
a(ti) + A v(ti) = B ; a(ti) = B -A v(ti) (1)
a = Dv / Dt = ( v(ti+1) -v(ti)) / Dt ; v(ti+1) = v(ti)) + a(ti) Dt (2)
On donne un extrait de la feuille de calcul :
| t(s) | v (m/s) | a (m s-2) | | 0 | 0 | 8,23 | | 0,05 | 0,41 | 4,74 | | 0,10 | 0,65 | 2,73 | | 0,15 | 0,79 | 1,57 | | 0,20 | 0,86 | 0,91 | | 0,25 | 0,91 | 0,52 | | 0,30 | ........ | 0,30 | | 0,35 | 0,95 | ....... | | 0,40 | 0,96 | 0,10 | | 0,45 | 0,96 | 0,06 | | 0,5 | 0,97 | 0,03 |
Le pas est Dt = 0,05 s.
Calcul de la vitesse v6 à t = 0,30 s.
v(ti+1) = v(ti)) + a(ti) Dt
v6 = v5 + a5 Dt =0,91 + 0,52*0,05 =0,936 ~0,94 m/s.
Calcul de l'accélération a7 à t = 0,35 s.
a(ti) = B -A v(ti)
a7 =8,23 -8,41 v7 =8,23-8,48*0,95 =0,174 ~0,17 m s-2.
|
|